SPring-8, the large synchrotron radiation facility

Release Date

03 Dec, 2007

Basic geometry shows that you can not fill a plane periodically by closely packing building blocks with a 5-fold "pentagonal" structure – 3-fold, 4-fold, even 6-fold symmetry is OK, but not 5.  See Figure 1.  Thus about 20 years ago, the scientific community was surprised by the discovery of class of space-filling materials that had 5-fold symmetry.  The explanation was that they were not periodic – but only quasi-periodic – having a structure that repeated, but not with a fixed step size.  These beautiful new materials generated artistic and mathematical interest, but also forced a re-examination some basic physical principles, since periodicity is built into the foundations of much of materials science.   Their structure is now beginning to be understood with the help of a 6-dimensional system for crystallography.  Here we describe a first in-depth investigation into the microscopic atomic vibrations of these "quasicrystals".   In conventional periodic crystals, such vibrations, called phonons, reflect the fundamental symmetry of the structure.  What about in a non-periodic but ordered quasi-crystal?

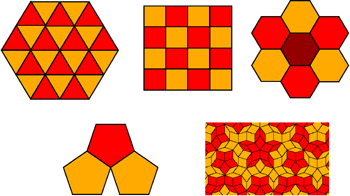Figure 1. Close packing of 3,4 and 6-fold symmetric structures can be used to fill a plane. However, 5-fold structures can not be stacked that way, one has to introduce an additional shape, and then the plane can be filled without translational symmetry.

The present work [1] from a multi-institutional, multi-national collaboration combines advanced experimental techniques and sophisticated calculations to provide a first clear picture of the vibrations of the atoms in quasicrystals.  One of the probes used was inelastic scattering, a demanding technique with very high resolution ΔE/E=10^-7, comparable to measuring a 1 km length with 0.1 mm precision.  This level of resolution is required to isolate the atomic vibrations of the material but is only possible in Japan at the very brilliant synchrotron radiation source, SPring-8.

The crucial component of this work is to compare quasicrystal with a fully periodic crystalline phase (called an approximant) based on the same fundamental structural unit as the quasi-crystal.  Figure 2 shows the construction of this unit.  When the largest cluster in fig 2, called a triacontahedron, is ordered in a cubic array one generates the crystalline approximant, while quasi-periodic ordering makes the quasicrystal.  

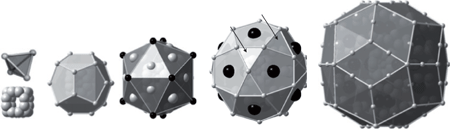Figure 2. Structure of the building block for i-ZnMgSc QC and its 1/1 Zn–Sc approximant. The formation of the successive shells of the triacontahedral cluster observed in both the 1/1 approximant and the QC: first a Zn tetrahedron, covered by a Zn dodecahedron followed by a Sc icosahedron, covered by a Zn icosidodecahedron and finally a Zn triacontahedron with atoms on vertices and mid-edges.

Figure 3 shows the results of measurements at SPring-8 superimposed on dynamics calculations using close to 3000 atoms, showing good qualitative agreement.  The slight blurring of the response for the quasi-crystal (right panel), as compared to the crystalline approximant (left panel) is visible.   Quantitative comparison is made in figure 4, where the full x-ray spectra are compared against calculation. The agreement is truly excellent given the complexity of the model, with nearly all of the features in the data also appearing in the calculations, with similar intensities.   The arrows indicate places where clear differences exist between the measured results for the QC and the approximant.  The general trend is that the more well-ordered a material, the stronger the tendency for their to be well defined modes at large momentum transfer and also the stronger the tendency to have a well defined gap (low intensity region) near 10 meV, more easily visible in Fig. 3.  One can consider these trends as being first steps from a crystalline response toward a glass-like response. 

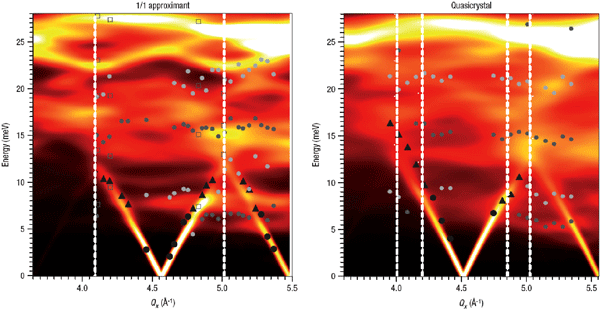Figure 3. Comparison between the measured dispersion relation and simulations with up to 3000 atoms. The simulation result is shown on a colour-coded temperature scale while symbols correspond to the positions of the excitations extracted from the inelastic X-ray spectra. The zone centers (Bragg points) are at 4.56 and 5.53 Å^-1 and the vertical dashed white lines indicate the position of the (pseudo-) Brillouin-zone boundaries.

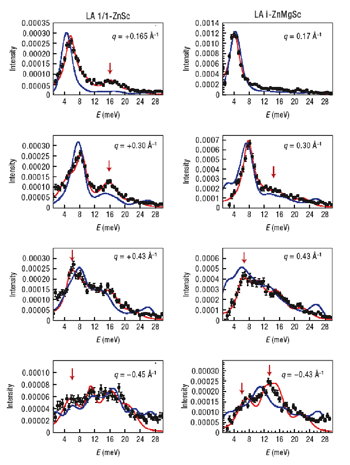Figure 4. Comparison between the experimental spectra and the simulations. Red lines are fits to the data (from which dispersion relations were extracted and used in Figure 2) and blue lines show the simulated response function S(Q, E ). Notice the visible broadening as q increases. The intensity distribution is well reproduced by the simulation. Note in particular the good reproduction of the longitudinal scans at + or -0.43 Å^-1. Arrows point to notable similarities and differences.

This work identifies the fingerprint of the quasi-crystalline phase as the reduced gap, and blurring out of the well-defined phonon modes.  The high quality of the data, and the excellent agreement between the calculations and the data, make this one of the first clear steps toward understanding the dynamics of this complicated, but important, class of materials.  It will eventually help to understand both the fundamental and thermal properties of quasi-crystals and aid in understanding the thermal properties of technologically important materials such as glasses.

Note:  Figures are from the Nature Materials paper.  These can be used if the paper is referenced.
Figure 2 is the top half of Fig. 1 of the Nature Materials paper.
Figure 3 is just Fig. 3 of the Nature Materials paper.
Figure 4 is is the right half of Fig. 5 of the Nature Materials paper.

[1] Marc de Boissieu, Sonia Francoual, Marek Mihalkovic et al., Nature Materials advanced online publication (2007).

Publication:
"Lattice dynamics of the Zn－Mg－Sc icosahedral quasicrystal and its Zn－Sc periodic 1/1 approximant"
Marc de Boissieu, Sonia Francoual, Marek Mihalkovi, Kaoru Shibata, Alfred Q. R. Baron, Yvan Sidis, Tsutomu Ishimasa, Dongmei Wu, Thomas Lograsso, Louis-Pierre Regnault, Franz Gähler, Satoshi Tsutsui, Bernard Hennion, Pierre Bastie, Taku J. Sato, Hiroyuki Takakura, Roland Currat and An-Pang Tsai
Nature Materials 6, 977 - 984 (2007), Published online: 4 November 2007

For more information, please contact Dr. Alfred Q.R. Baron (RIKEN/SPring-8 & JASRI/SPring-8):
baron@spring8.or.jp .