SPring-8, the large synchrotron radiation facility

Inquiry number

SOL-0000000909

Beamline

BL19B2 (X-ray Diffraction and Scattering II)

Scientific keywords

A. Sample category	inorganic material
B. Sample category (detail)	metal, alloy
C. Technique	X-ray diffraction
D. Technique (detail)	wide angle scattering
E. Particular condition	surface, room temperature
F. Photon energy	X-ray (4-40 keV)
G. Target information	dislocation, strain

Industrial keywords

level 1---Application area	mechanics, construction, industrial material
level 2---Target	Steel
level 3---Target (detail)
level 4---Obtainable information	residual stress
level 5---Technique	diffraction

Classification

A80.20 metal ・material, M10.80 stress strain

Body text

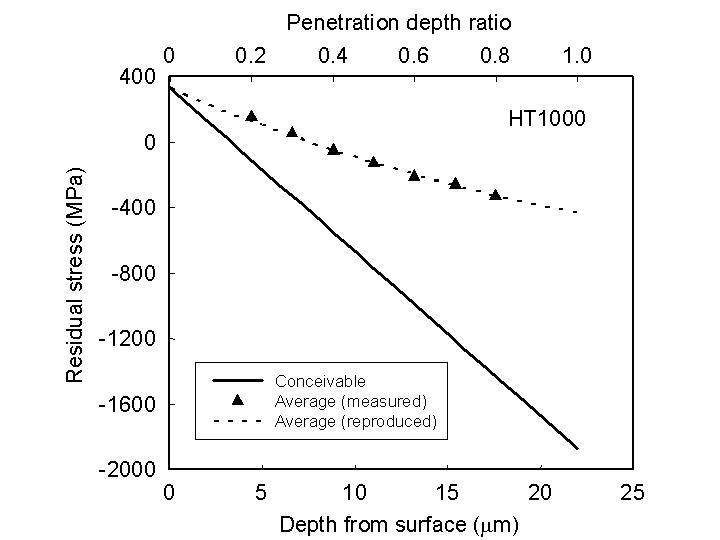
In this solution, X-ray diffraction was applied to steel treated by laser-peening to analyze depth profile of residual stress at the surface. By controlling incident and take-off angle of X-rays to the sample surface, penetration depth of X-ray is tuned. These data reveal the dependence of the process on the depth profile of residual stress at the surface treated by laser-peening.

Depth profile of residual stress in steel treated by laser-peening

Source of the figure

Bulletin from SPring-8

Bulletin title

SPring-8　Experimental Report No.13 (2004A)

Page

p.111

Technique

X-ray residual stress measurement is performed by observing dependence of scattering angle on sample orientation to incident X-ray. This technique enables non-destructive observation of depth profile of residual stress in sample.

Source of the figure

No figure

Required time for experimental setup

9 shift(s)

Instruments

Instrument	Purpose	Performance
Multi-axis diffractometer	X-ray diffraction measurement	4axes and 2axes

References

Related experimental techniques

Questionnaire

This solution is an application of a main instrument of the beamline.

Ease of measurement

Middle

Ease of analysis

Middle

How many shifts were needed for taking whole data in the figure?

Four-nine shifts